Macro-pKa
Accurate, physics-based modeling of the aqueous ionization and speciation behavior of small molecules

Accurate, physics-based modeling of the aqueous ionization and speciation behavior of small molecules
Macro-pKa is an automated solution for predicting macroscopic pKa values and pH-dependent tautomeric populations of ligands that combines physics-based DFT calculations with empirical corrections.
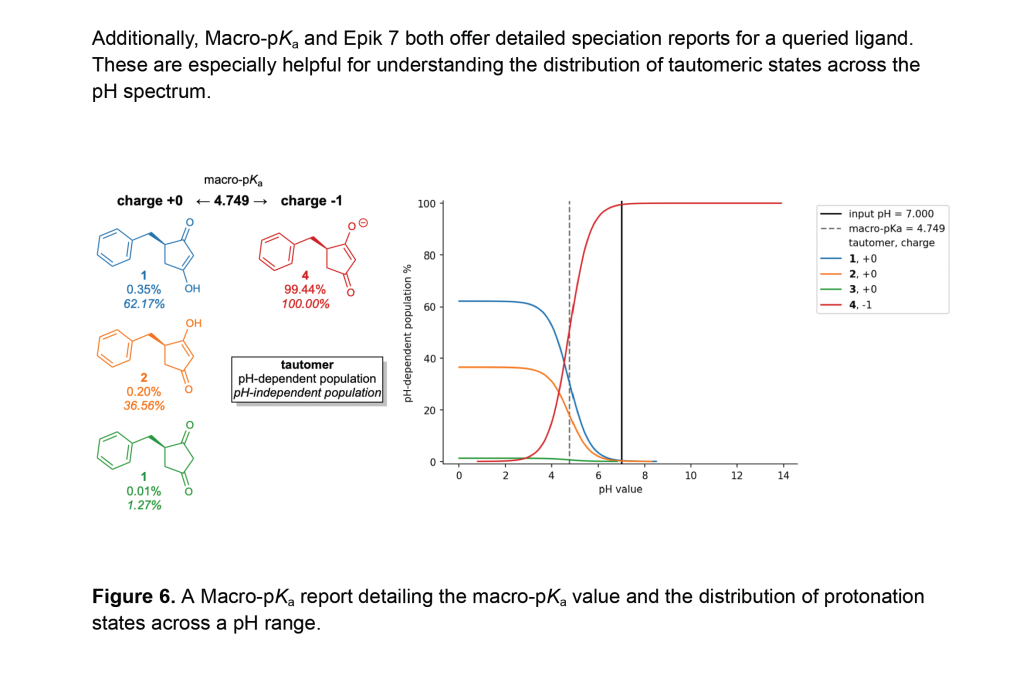
Learn about the various solutions for predicting pKa values, protonation state distribution, and derived properties that can be applied across a range of drug discovery stages, from screening through lead optimization.
Read the white paper
Learn more about the related computational technologies available to progress your research projects.
Quantum mechanics solution for rapid and accurate prediction of molecular structures and properties
Conformationally-dependent spectroscopic characterization based on quantum mechanics calculations
Browse the list of peer-reviewed publications using Schrödinger technology in related application areas.
Level up your skill set with hands-on, online molecular modeling courses. These self-paced courses cover a range of scientific topics and include access to Schrödinger software and support.
Learn how to deploy the technology and best practices of Schrödinger software for your project success. Find training resources, tutorials, quick start guides, videos, and more.